The following is a brief excerpt (pages taken from ‘The physics of golf’ (2nd ed.), by Theodore P. Jorgensen. (It explains D-Plane, and it’s practical application.)
I’m sorry about the long post, but think it’s good to have some reference material to make sure everybody is talking about the same stuff 
The D Plane
Euclid, the famous geometer, says something to the effect that two intersecting lines determine a plane. The normal to the clubface and
the line along which the clubhead is moving at impact intersect at the ball and therefore determine a plane. The line along which the ball
leaves the clubhead also lies in this plane. We shall call this plane the D plane because it is descriptive of the collision between the clubhead
and the ball.
Consider a collision for which the clubhead at impact is moving directly toward the chosen target and the normal to the clubface is
directed to a point exactly above the target. The D plane for such a collision contains the target, and the plane is vertical. After the colli-
sion, the ball will be moving in this plane toward the target with the line of flight a little below the normal to the clubface…
Equations Give Some Results
After the speed of the clubhead is given, the mathematical equations may be used to determine approximately what is happening after the
collision is over. They will tell us the speed of the clubhead, the speed and direction of the flight of the ball, and the rate of spin of the ball.
The velocity vector of the flight of the ball after the collision is below the normal to the clubface at impact. For similar swings the angle
between these two vectors increases almost directly with the loft of the club.
The rate of spin of the ball depends directly on the speed of the clubhead at impact. The golfer who can move the clubhead at a higher
speed will put more spin on the ball, and consequently, the ball will experience a greater lift. The lift will be greater because it increases
with the spin of the ball and it also increases with the speed of the ball through the air. With the greater lift, the ball will be held up longer, it
will not fall as fast, and with the higher speed it will fly farther before it hits the ground. This is true even though the drag also increases with
the speed of the ball.
The rate of spin of the ball depends directly on the speed of the ball as it leaves the club and almost directly on the angle between the
normal to the clubface and the line of the flight of the ball as it leaves the club. For a given speed of the ball, the spin rate is about three times
greater with a five iron and about five times greater with a nine iron than with a driver.
Collision Theory
The theory of collisions indicates that if a very light perfectly elastic ball is hit with a very heavy club with no loft, the ball will leave the
clubhead with almost twice the speed of the clubhead before impact. This is an upper limit. For the ordinary ball and an ordinary club, the
ball will be sent off at a slower speed. For a driver, five iron, and nine iron, the factors are 1.46, 1.30, and 1.12 for the three clubs, respec-
tively, according to our theoretical results. The photograph of Bobby Jones swinging his driver [4] shows the ball’s speed to be 1.4 times the
clubhead’s speed before impact. The agreement between 1.4 and 1.46 is better than we have any reason to expect because of possible experi-
mental error in determining the speeds involved and also in determining the coefficient of restitution of the golf ball. The agreement
suggests, however, that our theoretical results are not too far out of line. We may use the theoretical results to calculate the rate of spin of the
ball. Some experimental determinations of both the rate of spin and the speed of the ball are available [7]. These data are for the swing of a five
iron by a professional golfer, and the exact orientation of the clubface at impact is not given. By using a 5 deg angle between the normal to the
clubface and the line along which the ball leaves the clubface and a ball speed of 145 ft per second for a five iron, the theory gives a calcu-
lated rate of spin of 72 revolutions per second. For a five iron the measured spin rate for this ball speed averaged about 80 revolutions
per second. Perhaps a difference of this magnitude should be expected as a result of the approximations made in setting up the original math-
ematical expressions.
The spin put on the ball when it is hit correctly, so that it rolls up the clubface during the collision, is such that it appears to rotate in a
counterclockwise sense as seen by an observer facing a right-handed golfer. The ball is given what has been called underspin. A ball must
rotate with underspin in order that the aerodynamic forces give the ball the necessary lift. If the ball is hit with the edge of the club above the
center of the ball, the ball will be given topspin. Such a topped ball will have negative lift. This negative lift accounts for the quickly diving
flight of a topped ball. When the ball is hit out of deep rough and a layer of grass lubricates the contact between the clubface and the ball, there
may not be enough friction to give the ball the usual amount of spin. Under this condition the ball may leave the clubface along a line closer to
the normal than usual. Expert golfers have learned that a nine-iron shot from deep rough will not bite the green as does a shot with the
usual amount of backspin.
The D Plane as a Practical Tool
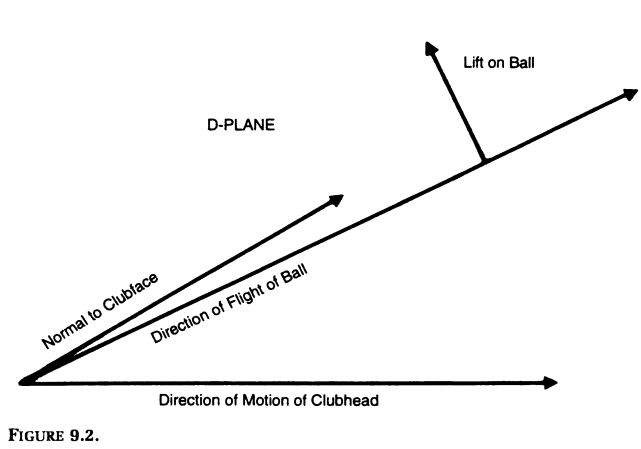
The D plane for a golf swing contains the path along which the clubhead is moving at impact, the normal to the clubface, and the initial
path of the ball after impact. The D plane also contains the aerodynamic lift force, since the lift force is perpendicular to the axis of spin
and this axis is perpendicular to the D plane. A diagram of the D plane for a possible five-iron shot is given in Fig. 9.2. A copy of this diagram
on a card will facilitate the reading of the following discussion.
It is suggested that a golfer take a five iron in hand as he reads this description of the use of the D plane. If the reader takes the usual
stance with a five iron and swings the club directly in the direction of an assumed target with the clubface square to the target, neither toed in
or toed out, then the D plane for the swing will be a vertical plane containing the velocity of the clubhead, the velocity vectors of the ball
and the normal to the clubface, and the target. To illustrate this swing, the card representing the D plane should be held so that the line repre-
senting the clubhead motion points horizontally toward the target and the line representing the normal to the clubface points directly toward
but above the target. For such a swing, in the absence of a crosswind, the ball will fly directly toward but above the target without a hook or
a slice.
Next, let the reader open the face of the club so that the normal to the clubface points to the right and above the target. The club has been
toed out. This is done while retaining the original intention of swinging the club directly at the target. To represent this swing of the
club, the D plane is tilted to the right. The line representing the direction of the clubhead motion is still horizontal and points toward the
target. The line representing the normal to the clubface points above and to the right of the target. The card shows that the path of the ball
will also be to the right of the target but not as far to the right as the normal to the clubface. Since the lift force lies in the D plane, the lift
force will have a component to the right, and this component will produce a slicing motion of the ball.
For a club that has been toed in, the D plane is tilted to the left, and the previous discussion applies except that “left” replaces “right” and
the component of the lift force to the left will produce a hooking motion.
Many swings with a golf club are made in which the clubhead is not directed toward the intended target. For such swings, the line on the D
plane card representing the direction of the clubhead motion, while still horizontal, must be directed either to the right or to the left of the
target. If the swing is described by a vertical D plane, the ball will go to the right or to the left without hooking or slicing. The reason for this is
that the horizontal component of the normal to the clubface also points along the direction of the clubhead motion. However, if for these cases
where the clubhead motion is not toward the target, and the clubface is toed out or toed in, the D plane is tilted as before, and the ball will have
a slicing or a hooking motion.
It is usually taught that a swing of a clubhead from outside in will produce a slice, but we see that a slice will result only if the swing can
be described by a D plane tilted to the right, and if the D plane is tilted to the left, the ball will have a hooking motion in spite of the motion of
the clubhead from the outside in.
The analysis involving the D plane may be used in diagnosing any swing producing an aberrant flight of the ball. Consider the problem
facing a young man who played a round of golf with me. His tee shots consistently started off to the left and sliced back to the right. The
slicing flight of the ball tells us that the D plane for his tee shots was tilted to the right; the aerodynamic lift force had a component to the
right producing the slice. Since the ball started off along a line to the left of the target and this line is in the D plane, we know that the
clubhead at impact was also moving along a line pointing to the left of the target. Since the normal to the clubface is in the tilted D plane and
lies above the line along which the clubhead is moving at impact, the normal to the clubface must point to the right of this line. We have thus
determined that the young man was swinging the clubhead from the outside in across the line to the target and the face of the club was open
to the path of the clubhead. Our diagnosis was confirmed when on one of the tees, his driver cut through the grass below his ball. The grass
was removed along a path pointing several degrees to the left of the green. A diagram of the tilted D plane for this kind of shot is shown in
Fig. 9.1.
The analysis involving the D plane may also be used to design swings to produce intentional hooks and slices. The club must be toed
in or toed out to tilt the D plane to the left or right. If the ball is to be kept in the fairway, the line along which the clubhead is swung must
be pointed to the right of the target for the intentional hook and to the left for the intentional slice. Figure 9.1 shows how the D plane must be
oriented for the intentional slice.
Many golf instruction books treat the subject of sidehill lies. When the ball lies lower than your feet, you are to play for a slice, and when
the ball lies higher than your feet, you are to play for a hook. The D plane may be used to understand why. Consider a sidehill lie with the
ball higher than your feet. If you stand to the ball with your usual stance, the normal to the clubface will naturally point to the left of the
target. This will tilt the D plane to the left, and the ball will have a hooking flight. The golfer has two possible ways to correct this flight of
the ball. He may, as the books advise, play for a hook and aim to the right of the target. The question is, How much to the right of the target
should he aim? He may toe the club out a bit so that the normal to the clubface and the direction of the motion of the clubhead at impact
indicate a D plane that is vertical and contains the target. There will be no hook for a vertical D plane, but the toeing out of the club will give
the club more loft. Thus for a given swing the ball will not go as far as one might expect for a given club. Then the question is, How far will
the ball go? In either case the shot requires considerable judgment. In considering what happens when the clubhead meets the ball, we
have assumed that the ball makes contact with the center of the clubface, at the “sweet spot.” For such a shot there is no torque about the
shaft of the club to produce a change in the orientation of the clubface.
If the ball makes contact with the clubface off-center, the clubhead will turn under the torque produced by the large force between the club-
head and the ball. If the ball is hit too close to the toe of the club, the club will turn to a toed-out position before the ball leaves the clubhead,
putting the normal to the clubhead farther to the right than was intended. The ball will then fade to the right.
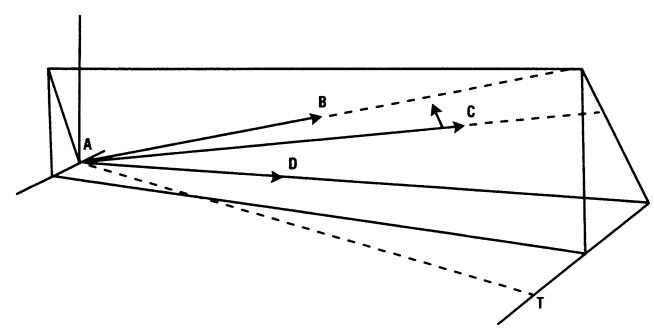
FIGURE 9.1. The plane containing three directed line segments represents the D plane for a slicing golf shot. In the diagram the ball is on the
tee at A. The line AT represents the line from the ball to the target. The line AB represents the normal to the clubface at impact with
the ball, the line AD represents the velocity vector of the clubhead after impact, and the line AC represents the velocity vector of the
ball just after impact. For this shot the clubhead is moving from the outside in across the line from the ball to the target, and the ball
will start off to the left of the target line and slice back toward the target line, since the lift vector is tilted to the right.
. It makes a lot of sense to the original question about draws going shorter, and when thinking that a steeper angle of attack causes hooks/draws, but doesn’t add up when looking at the above comment regarding draws rolling more because of less backspin. If a draw is caused by a steeper angle, and a steeper angle causes more backspin, then it all seems a little crazy don’t you guys think?
RR