robbo,
Golf is an intriguing sport. It forms an interesting mosaic containing many paradoxes. There are those who teach or taught an early release from the top - e.g., a Peter Croker or the late Tom Tomasello. Brian Manzella refers to it as 'drop and catch '. But also those teaching just the opposite, indeed asking to make a deliberate effort to not release the club - Mark Evershed and Paul Bertholy come to mind. Retaining the angle is not all that easy as anyone can readily experiment for himself. Just swing at normal speed and do all that you can muster to retain the angle right through impact and beyond. Darned large torque to fight.
There is some interesting anecdotal information on this subject in 'The Physics of Golf ’ by the late Prof. Jorgensen -
“A friend and I were discussing this subject when he asked me whether I had a club that he could swing to feel this large torque. We stepped out onto the patio with a driver. He took a few practice swings, and then told me he was going to swing the club keeping his wrists cocked throughout the swing. This he did. To his utter amazement the shaft broke in his hands near the lower part of his grip and the clubhead and most of the shaft flew out over the garden. … I have not sacrificed another club to discover the size of this torque.”
It is not easy to analyze mathematically in true 3D as it is rather complex and it really requires experimental back up to tweak and adjust the assumptions to be made in any realistic 3D mathematical model. But we are here not to find the precise behaviour but rather to get some first order impression, an order of magnitude, of such retaining torque. For this purpose a simple planar double pendulum model will suffice. Hence it is assumed that arm and club are contained in one plane and hence also no roll of the arm.
We assume the inner arm to have a length of 0.6 m and a mass of 6 kg. The club is approximated by a slender homogeneous shaft, 1 m long with a mass of 0.11 kg and the clubhead is taken to be a point mass of .26 kg. This could perhaps be a 5 iron.
The inner torque is taken as a constant torque of 80 Nm. This torque would give for a normal release an maximum clubhead of about 80 miles/hour. It will be somewhat less when the angle is actually retained throughout the whole down swing. But the mathematical golfer than also completely misses the ball as he swings over it.
In the mathematical model the wrist torque is calculated to produce at each moment the exact opposite of the torque developed at the joint and when applied in the model as an external torque produces than a complete and total angle retention throughout the swing.
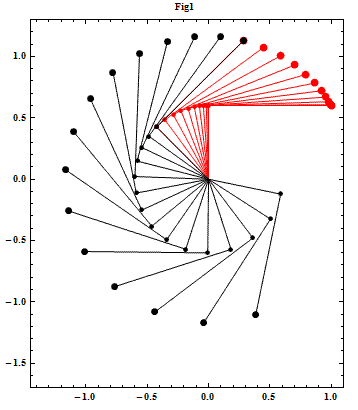
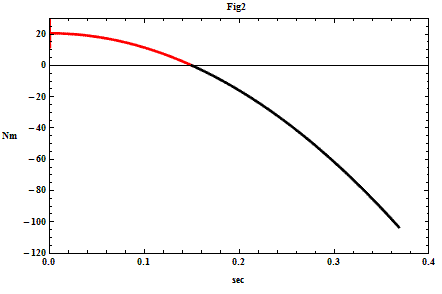
Figs 1 and 2 respectively show the swing and the associated retaining wrist torque. The retaining torque gets indeed very hefty. In English units, 75 lb-ft. Hence a torque created by a force of 75 lb acting perpendicular at a distance of 1 ft from the pivot. I wonder if someone can produce such a big torque with the wrists. Well just try it - take a rigid light rod of about 3 ft and attach 25 lb at one end and try keeping the rod horizontal with your wrists acting at the other end. 
Notice in Fig 2 that the retaining torque changes polarity during the down swing. First the clubhead tries to move closer to the pivot (red) and than when some angular speed is developed the clubhead enter into its release cycle (black). In this particular case however release, either way, does not happen due to the action of the applied retaining torque.
RR
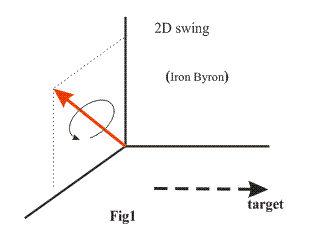
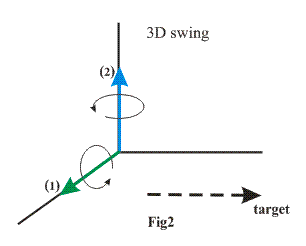It is perhaps interesting and useful to distinguish between two type of swings as shown very schematically in Figs 1 and 2.
RR